appunti-steffo/2 - Algoritmi e strutture dati/1 - Appunti/04 - Notazione asintotica.md

# Notazione asintotica

La _notazione asintotica_ è un sistema per **stimare** velocemente il costo di un algoritmo complesso.

Ci permette di **confrontare velocemente il caso peggiore** degli algoritmi.

In particolare, consideriamo il _rapporto tra il numero di operazioni nel caso peggiore e la dimensione dell'input_.

## Limiti

Possiamo dare a questa stima dei limiti, superiore e inferiore, che rappresenteranno rispettivamente un costo che non sarà **mai superato** e un costo che verrà **sempre superato**.

Chiameremo questi limiti _upper bound_ e _lower bound_; la loro combinazione darà un _tight bound_.

L'obiettivo sarà di _ricavare i bound più precisi possibile_ per un dato algoritmo, ovvero l'**upper bound più basso** e il **lower bound più alto**.

### O grande

> "O grande"  
> O di g(n)
> "big-O"

Per rappresentare la stima, useremo una notazione particolare, detta _O grande_, con la seguente proprietà:
- Date due funzioni `f(n) : N -> R` e `g(n) : N -> R`, diremo che `f(n) ∈ O(g(n))` se e soltanto se `∃ c > 0, n ≥ n_0` tali che `∀ n ≥ 0, f(n) ≤ c * g(n)`

Quando una funzione è O grande di un altra, significa che **asintoticamente, la funzione in O grande è sempre maggiore di quella che sta venendo stimata**.

> **Ipotesi**  
> - `f(n) = 2n² + 3n + 6`  
> - `g(n) = n²`
>
> **Tesi**  
> - `f(n) ∈ O(n²)`.
>
> **Svolgimento**  
> Scrivo una disequazione, lasciando intatto il termine noto:  
> 1. `2n² + 3n + 6 ≤ 2n² + 3n² + 6`  
> 2. `n² ≤ 2n² + 3n² + n² = 6n²` per `n ≥ 3`
>
> Sappiamo, allora, che `2n² + 3n + 6 ≤ 6n²`.

#### Espressioni di O grande

Questa tabella rappresenta le espressioni di O grande più comunemente utilizzate, in ordine **dalla più forte alla più debole**.

> Più forte significa che, per ogni riga della tabella, tutte le righe sottostanti sono contenute nell'espressione.
>
> Ad esempio, `O(n) ∈ O(1)`.

| Espressione O() | Nome |
|-----------------|------|
| `O(1)` | Costante |
| `O(log log n)` | loglog |
| `O(log n)` | Logaritmica |
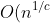| ![LaTeX](https://latex.codecogs.com/png.latex?O(n^{1/c})) (per c ≥ 1) | Sublineare |
| `O(n)` | Lineare |
| `O(n log n)` | nlogn |
| `O(n²)` | Quadratica |
| `O(n³)` | Cubica |
| `O(n^k)` (per k ≥ 1) | Polinomiale |
| `O(a^n)` (per a ≥ 1) | Esponenziale |
| `O(n!)` | Fattoriale |

#### Polinomiale

Molto spesso, noteremo che il tempo richiesto da una funzione è O grande di un polinomio di grado K, ovvero `f(n) ∈ O(n^k)`.

Notiamo che in questi casi, possiamo semplificare l'O grande al grado massimo del polinomio.

> Ad esempio, `O(n² + n + 1) = O(n²)`.

##### Dimostrazione

Per `n > 0 \and 0 ≤ i ≤ k`:  
![LaTeX](https://latex.codecogs.com/png.latex?a_k%20n^k%20+%20a_{k-1}%20n^{k-1}%20+%20%E2%80%A6%20+%20a_1%20n%20+%20a_0%20%E2%89%A4%20|a_k|%20n^k%20+%20|a_{k-1}|%20n^k%20+%20%E2%80%A6%20+%20|a_1|%20n^k%20+%20|a_0|%20n^k%20=%20(|a_k|%20+%20|a_{k-1}|%20+%20%E2%80%A6%20+%20|a_1|%20+%20|a_0|)%20n^k)

#### Proprietà di O grande

1. `f(n) ∈ O(g(n)) -> ∀ a > 0, a * f(n) ∈ O(g(n))`.
2. `f(n) ∈ O(g(n)), d(n) ∈ O(h(n)) -> f(n) + d(n) ∈ O(g(n) + h(n)) -> O(max\{g(n), h(n)\})`
3. `f(n) ∈ O(g(n)), d(n) ∈ O(h(n)) -> f(n) * d(n) ∈ O(g(n) * h(n))`

In pratica, se una funzione è la _somma di più termini_, basta guardare l'**`O()` più grande** tra tutti i suoi termini; se invece una funzione è un _prodotto di più termini_, si possono **omettere le costanti**, e l'`O()` finale sarà dato dal **prodotto degli `O()`** dei termini.

## Lower bound

Possiamo anche stimare il _lower bound_, il limite inferiore: il **numero minimo di operazioni** che viene effettuato **nel caso migliore** con la **massima dimensione dell'ingresso**.

### Ω()

> "Omega"  
> Omega di g(n)
> "big-Omega"

Esiste un equivalente di O grande per il lower bound: è detto _Omega grande_, o più semplicemente _Omega_, e funziona nello stesso identico modo, solo... al contrario.

Diremo che `f(n) ∈ Ω(g(n))` se e solo se `∃ c > 0, n_0 ≥ 0 : ∀ n ≥ n_0 f(n) ≥ c * g(n)`.

#### Espressioni di Ω()

Anche in questa tabella le espressioni sono **dalla più forte alla più debole**.

| Espressione Ω() | Nome |
|-----------------|------|
| `Ω(n!)` | Fattoriale |
| `Ω(a^n)` (per a ≥ 1) | Esponenziale |
| `Ω(n^k)` (per k ≥ 1) | Polinomiale |
| `Ω(n³)` | Cubica |
| `Ω(n²)` | Quadratica |
| `Ω(n log n)` | nlogn |
| `Ω(n)` | Lineare |
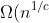| ![LaTeX](https://latex.codecogs.com/png.latex?\Omega(n^{1/c})) (per c ≥ 1) | Sublineare |
| `Ω(log n)` | Logaritmica |
| `Ω(log log n)` | loglog |
| `Ω(1)` | Costante |

## Tight bound

Quando **upper e lower bound coincidono**, allora otteniamo un _tight bound_.

### θ()

> "Theta"  
> Theta di g(n)
> "big-Theta"

Anche per il tight bound abbiamo una notazione equivalente a O grande e Omega grande: _Theta grande_!

Diciamo che `f(n) ∈ θ(g(n))` se e solo se `∃ c_1, c_2 > 0, n_0 ≥ 0 : ∀ n ≥ n_0, c_1 * g(n) ≤ f(n) ≤ c_2 * g(n)`.

Ha la particolarità che non valgono tutte le proprietà degli altri due: va usata quindi con cautela!

## Risorse utili

[khanacademy.org](https://www.khanacademy.org/computing/computer-science/algorithms/asymptotic-notation/a/big-big-theta-notation)